誘電率について知ろう
液晶材料を深く知るうえで非常に重要な物性値が誘電率です。誘電率を知るために、物質の電気的な性質について学んでいきましょう。
導体と絶縁体の違い
電気を通す物質を導体と呼びますよね。正確に言えば、自由電子が多く電気伝導率が大きい(=抵抗値が小さい)物質を導体と呼んでいます。
一方、電気を通さない物質を絶縁体(不導体)と呼びます。
こちらも正確に言えば、自由電子が少なく電気伝導率が小さい(=抵抗値が大きい)物質を絶縁体と呼びます。
では、導体と絶縁体の境目はどこにあるのでしょうか?
実は、これに対する明確な答えは無いようです。
例えば、絶縁体を研究している人は、少しでも電気を流せば導体と言うでしょう。
一方、導体の研究をしている人にとっては、少し電気を流したくらいでは、導体では無いと言うかもしれません。
液晶は絶縁体
話を液晶に戻しましょう。さて、液晶材料は導体でしょうか?それとも絶縁体でしょうか?
正解は絶縁体です。
不純物の無い液晶材料が用意できたなら、抵抗値は1×1012Ω(1PΩ)くらいはあるんじゃないかと思います。
つまり、液晶材料は、自由電子が少ないために電気をほとんど通しません。
絶縁体は誘電体である
分極という現象を示し、誘電率というパラメータを持つ物質を、誘電体と呼びます。誘電体は、絶縁体でなくてはいけません。
つまり、絶縁体(電気が流れにくい物質)であることが誘電体となりうる条件です。
誘電体は分極する
細かいことはを完全に無視して、ざっくりと説明します。誘電体とは何かと言うと、分極現象が生じる物質のことです。
言い換えれば、誘電体でなければ分極が起きません。
その理由を説明していきましょう。
分極とは
分極という現象をざっくり説明すると、双極子モーメントが揃ったことによって生じる現象です。じゃあ、双極子モーメントが何かというと、一対の正負の電荷や磁荷が作り出すベクトルのことです。
一対なので、正負があり、負から正に向かってベクトルが定義できるのです。
ベクトルなので、双極子モーメントは方向と大きさの要素を持っています。
図で書くときはマイナスの電荷からプラスの電荷への矢印で表します。
分極が巨視的(マクロ)な現象だとすると、微視的(ミクロ)な現象が双極子モーメントの発現です。
ざっくり言ってしまえば、原子や分子レベルでの電荷の偏りを指します。
分極は、そのの違いによって、3つの分極に大別されます。
分子分極
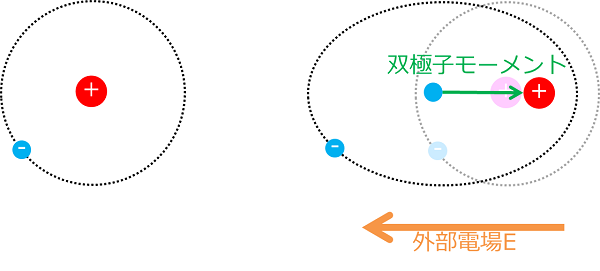
物質を構成する分子、その分子を構成する原子、その原子を構成する原子核と電子雲に偏りが生じる分極です。原子核は重くて動きにくいですが、電子は軽いので、外部から電場をかけたときに、
電子雲の中心が原子核の位置からずれて双極子モーメントが発現し、分極が生じます。
イオン分極
イオン分極はイオン結晶でのみ生じる分極です。イオン結晶ではプラスイオンとマイナスイオンが、その構成元素になりますが、プラスイオンとマイナスイオンの変位によって生じる分極のことです。
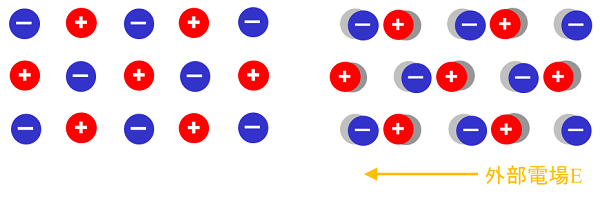
配向分極
物質を構成する分子において、その分子内部で双極子モーメントが発現し、分子の向きが変わることで生じる分極です。
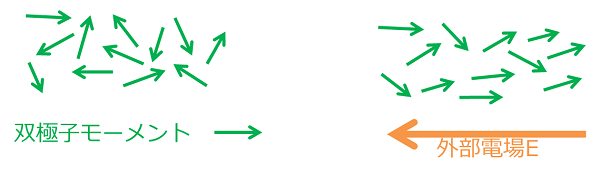
分極する・しない
物質の両端に電圧を加えたとき、導体、誘電体ともに、電荷の偏りが生じますが、そのメカニズムは異なります。導体では、電荷の偏りは自由電子によって生じます。
自由電子はその言葉の通り、自由に動き回ります。しかも素早く動きます。
よって、電圧が加えられた途端、物質表面に自由電子が集まります。
そのため、物質内部だけを考えると、電荷の偏りはありません。
一方、誘電体では、電荷の偏りは分極によって生じます。
分極は物質を構成する分子や原子の構造や配列が変化する(双極子モーメントが並ぶ)ことで起こります。
つまり、物質表面に限らず、全体に渡って電荷の偏りが生じます。
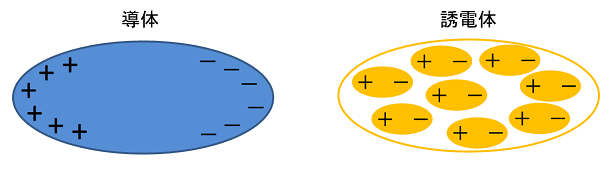
別の側面から言い換えて説明してみましょう。
導体は、自由電子が豊富に存在するため、分極が起こせないとも考えることができます。
外部からの電圧(電気エネルギー)があったとしても、そのすべてが自由電子を動かすために使われてしまうので、
別の用途、分極を起こすために使うことができないのです。
一方、誘電体は、自由電子がほとんどありません。
外部からの電圧(電気エネルギー)は、自由電子を動かす以外の用途に使われる必要があります。
そういった理由で分極を起こして電気エネルギーを消費すると考えることもできるでしょう。
また、分極というのは、電子雲が動いたり、配向が変わるなど、構造の変化を伴います。
自由電子は動くのが容易なので緩和しやすいですが、構造の変化はそうはいきません。
つまり誘電体は、電荷の偏り(電気エネルギー)を溜め込むことができます。
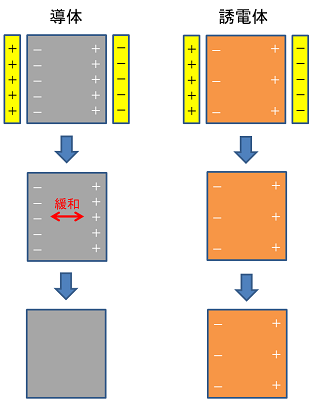
分極の周波数依存性
先ほど説明した3種類の分極は、分極が生じる周波数が違います。ミクロな分極は高周波に近い領域でも生じますが、マクロな分極になればなるほど低周波に近くなります。
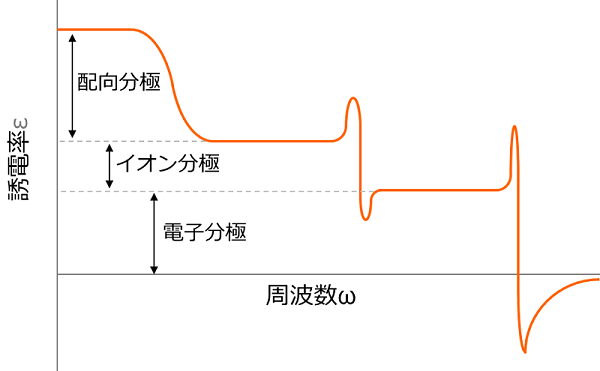
液晶で重要なのは配向分極
液晶で分極といった場合、ほとんどの場合、配向分極のことを言います。つまり、低周波側で生じる配向分極で、液晶の配向(向き)が変わって揃います。
逆に考えれば、高周波では液晶の配向は変わらないことになります。
一度、要点をまとめます。
・液晶は、絶縁体=誘電体です。
・液晶は、誘電体なので分極現象が生じます。
・液晶は、分極現象のうち配向分極が主として生じます。
・液晶は、高周波領域では分極による配向が起きません。
自発的に分極する誘電体がある
外部から電場を印可することで、分極が誘起されることを説明しました。この場合、電場を印可しない限り、誘電体は分極していないことになります。
このように外部電場などの外部エネルギーを加えない限り分極しない誘電体を「常誘電体」といいます。
一方、この世の中には、何もしなくても勝手に分極している誘電体が存在します。
外部電場などの外部エネルギーを加えなくとも、自発的に分極している誘電体を「強誘電体」といいます。
液晶にも強誘電体になるものがあり、強誘電性液晶と呼ばれます。
強誘電性液晶の話は、また別途、詳しく説明します。
誘電率
さて、誘電体の性質に関する話に戻りましょう。誘電体の性能の高さは誘電率という物性値で表します。
誘電率をざっくり言ってしまえば、どれだけ分極するか?です。
たくさん分極する。つまり、電荷の偏り具合が大きいと、誘電率は高くなります。
誘電率には方向性がある
双極子モーメントがベクトルであることを説明しました。ベクトルなので、大きさと方向があります。分極は双極子モーメントによって生じるので、分極も大きさと方向があります。
誘電率は分極によって生じるので、これまた大きさと方向があることになります。
ある方向から見ると誘電率が大きいが、ある方向から見ると誘電率が小さいなんてことも起きます。
つまり、誘電率は方向性があります。
ここでは、最も一般的なネマティック液晶の誘電率を例にとって、説明していきます。
この誘電率の方向による差異を表したものを、誘電率楕円体と呼び、ラグビーボールのように図示します。
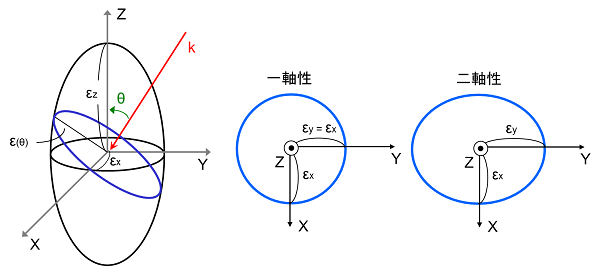
液晶分子1個が全く動かない状態では3次元的に異方的なので、
直交座標系においてX軸、Y軸、Z軸と分けて考えるとき、
ε X ε Y ε Zという3方向の誘電率を考えます。(二軸性の誘電率楕円体)
しかし、ネマティック相の時には、分子が短軸方向にクルクルと回転していますので、
短軸方向の誘電率は平均されて一様に見えます。(一軸性の誘電率楕円体)
また、ネマティック相ではなく等方相(液体状態)になると、液晶分子は全方向に対して回転をします。
つまり、短軸方向だけだった回転が、長軸方向にも起こるため、結果的にはすべての方向の誘電率が平均化され、
どの方向にも一様に見えます。(球状の誘電率楕円体)
今はミクロな分子1個に対して記述しましたが、これはマクロつまり液晶分子の集合体で考えた場合でも同じです。
ここで重要な点を説明します。 長軸方向の誘電率と短軸方向の誘電率が違う場合を誘電異方性があるといいます。
誘電異方性のことをΔε(デルタイプシロン)とも呼びます。
分子長軸方向の誘電率をε∥ 分子短軸方向の誘電率をε⊥ と書きますので、
誘電率異方性は、 Δε=ε∥ - ε⊥ と定義されます。
長軸方向の誘電率が大きい場合を「誘電異方性が正」といいます。
短軸方向の誘電率が大きい場合を「誘電異方性が負」といいます。
電荷の偏りは分子構造内の電子の偏りであるため、この誘電異方性の符号の違いは液晶分子の構造に依存しています。
さて、誘電率が大きいと、電荷の偏り具合が大きいと説明しました。
つまり、誘電率が大きいと外部電場による構造変化が大きく起こることになり、ほかの物性にも影響を与えます。
液晶を語る上で、重要な物性値として、屈折率があります。
なぜ重要かというと、液晶ディスプレイのように光を制御する場合、屈折現象が生じるためです。
誘電率が方向によって差異がある場合、屈折率にも同じように差異ができます。
つまり、誘電率楕円体と同じように屈折率楕円体を考えることができるわけです。
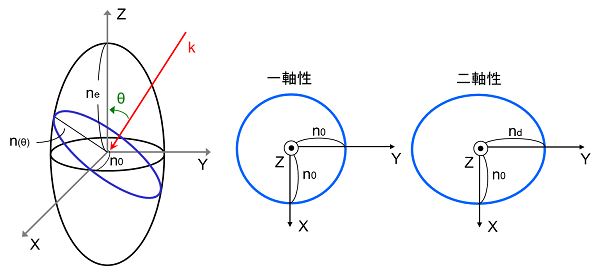
先ほど説明した通り、誘電率楕円体をある面で切った時、面内のどの方向でも同じ誘電率になる場合があるように、
屈折率楕円体をある面で切ったとき、面内で屈折率が一様になる面があります。
このとき、屈折率が一様になる面に対して、垂直な法線方向を、光軸と呼びます。
光軸から入った光は、屈折率が方向に依らず一様な空間を通り抜けます。
さて、光軸から入射した光にはどういった特徴があるのでしょうか?
皆さんがスネルの法則として勉強したように、もし、屈折率に差異があれば、光の伝搬速度に差異ができます。
また、屈折率が途中で変化すると、光の進む方向は屈折し、入射光は曲がります。
つまり、「光軸から入射した光は、屈折せずにまっすぐ進む。」とか、
「光軸から入射した光は、全方向の光が同じ速度で物質中を伝搬する。」と言い換えることができます。
一方、面内の方向によって屈折率が異なる(異方性がある)場合、先ほどとは反対のことが起きます。
つまり、「光軸以外から入射した光は、屈折する可能性がある。」、
「光軸以外から入射した光は、方向に依って異なる速度で物質中を伝搬する。」となります。
この光軸から入射する光のことを”常光”、光軸以外から入射した光を”異常光”と呼ぶこともあります。
ちなみに、誘電率において、Δε(デルタイプシロン)を誘電率異方性と呼ぶことを説明しましたが、
同じように屈折率においても、Δn(デルタエヌ)を屈折率異方性と呼び、Δn=ne - noと定義されます。
eは異常光線(extraordinary ray)の頭文字、oは常光線(ordinary ray)の頭文字です。
さて、このあたりで分極の話は終わりにしましょう。
光の伝搬などについては、別の章でも少し詳しく説明しようと思います。