いろんな偏光

この章では、偏光の種類について説明します。
そのために、まず、光というものが、どういったパラメータで記述されるかを知り、
様々な偏光が現れる条件を考えていきます。

光のパラメータ

光は粒子であり波であるというのは、非常に有名な特性です。
ここでは、光の粒子性は無視しておいて、波として考えていきます。
さて、波というのは、どのようなパラメータで記述することができるでしょうか？
まず、平面に描かれた波（平面波）というものを考えてみましょう。
図にすると次のようになります。


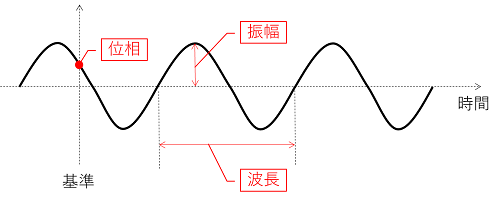
上図から分かるように、あるひとつの平面波を特定するには、振幅、波長、位相の3つが分かればいいことが分かります。
そして、位相だけが違う2つの同じ波があった場合、その位相の差を位相差といいます。


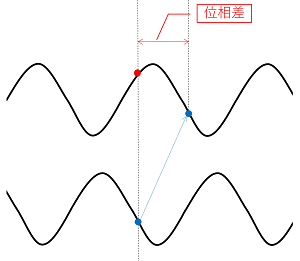
さて、ここまでは平面に描かれた波について考えましたが、これが空間上の波になるとどうなるでしょうか？
この場合、3次元のどの方向に波が振動しているか？という要素が増えます。
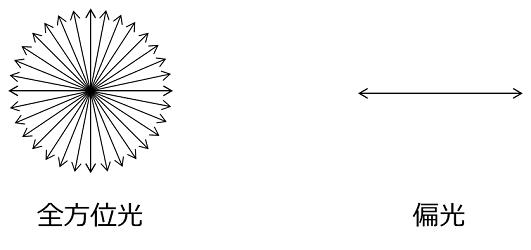
偏光の話から図を再掲しますが、波の進む方向から見た時に、3次元的に波が広がったものが全方位光。
一方向にのみ波が振動する場合の光は直線偏光と言います。

では、現実に存在する自然光（例えば太陽から放射されてくる光）を考えて見たいと思います。
しかし、自然光は様々な振幅、様々な波長、様々な位相、様々な方位を持った光となっています。
いろんな波長、いろんな位相の光というものを議論するのは大変なので、ある条件での話を考えます。
あるひとつの振幅、あるひとつの波長、あるひとつの位相を持った全方位光について考えます。

光はベクトルですから、ベクトルの合成や分解を行うことができます。
よって、全方位光を単純化して、直交する2つの直線偏光として考えることができます。
さぁ、同じ振幅、同じ波長、同じ位相の2つの直交した偏光を考えてみましょう。

直線偏光

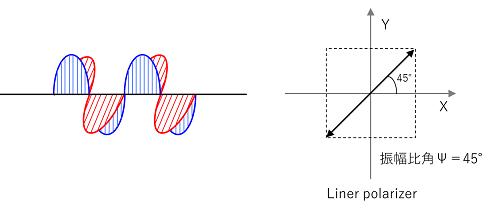
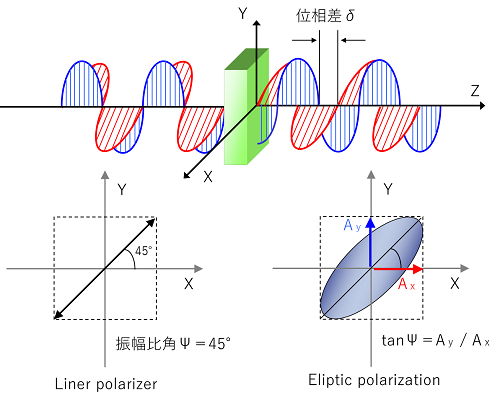
同じ振幅、同じ波長、同じ位相の2つの直交した偏光があるとして、この直交した偏光を合成してみましょう。
2つの直線偏光から45°だけ傾いた1つの直線偏光に合成されることが分かります。
つまり、同じ位相の光を合成すると直線偏光になることが分かりました。

楕円偏光と円偏光

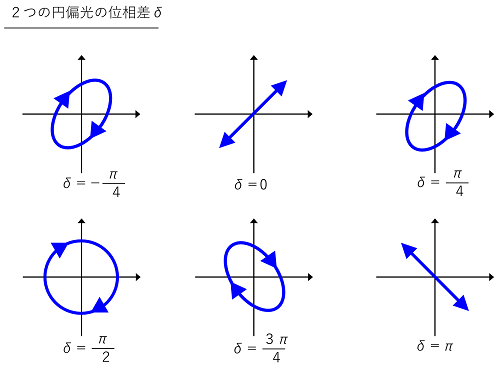
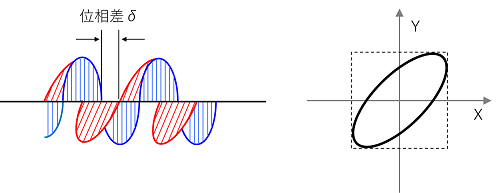
じゃあ、次は位相がずれた偏光（位相差のある偏光）を足し合わせる場合を考えましょう。
位相差のために、足し合わせた光は直線にならず、楕円になることが分かります。
ただし、楕円偏光のうち、2つの偏光の位相差が90度（π/4）もしくは270度（3π/4）の時には、
楕円が円になりますので、この時の楕円偏光だけを特別扱いとして円偏光と呼びます。

液晶に光が入射すると・・・

液晶がある一方向に配向している場合、長軸方向と短軸方向で屈折率の差異ができます。
屈折率の差異があるということは、液晶に入射した光は、長軸方向と短軸方向で、進む速度が変わります。
進む速度が変わるということは、出てきた時に位相差が生まれます。
つまり、直線偏光が液晶を通って出てきた時には楕円偏光や円偏光に変わるということです。
ただし、位相差が180°や360°であれば、直線偏光で出てくることになりますので、注意が必要です。

円偏光二色性（CD：Circular Dichroism）

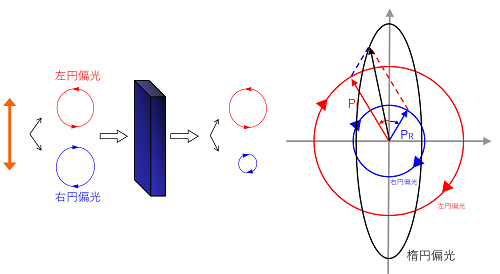
このように直線偏光が楕円偏光に変わることを違う切り口で説明してみましょう。
直線偏光は2つの円偏光を足し合わせたものと考えましょう。
何度も書きますが、光はベクトルなので、分解するのも自由なのです。
もし、液晶に入射した左円偏光と右円偏光に対して、左右の円偏光を吸収する能力に差があったらどうなるでしょうか？
下図のように実際に作図すれば分かりますが、円偏光の大きさに差ができると、楕円偏光が出来上がります。
この現象を円偏光二色性といいます。

旋光能（ORP：Optical Rotatory Power）

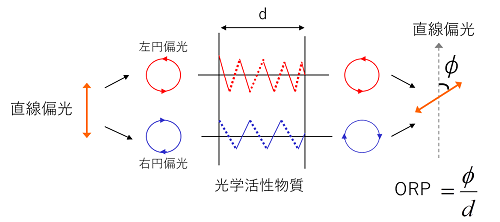
右円偏光と左円偏光に対して、屈折率に差がある物質を考えます。
もし、そのような物質に、位相差が同じ左右の円偏光を入射させるとどうなるでしょうか？
出てくる2つの円偏光に位相差ができますね。
この位相差によって、偏光の偏光面が回転する現象のことを”旋光性”といいます。
そしてこの旋光性の強さ、つまり、どれだけ偏光面を回転させられるかという能力を取って”旋光能”と呼びます。
旋光能は、単位距離あたりに対して定義されるため、旋光面が回転した角度Φを距離dで割って計算します。



左右2つの円偏光の位相差の大きさによって、直線偏光になるのか、楕円偏光になるのか、円偏光になるのか、
ということが決まります。一覧にすると、以下の図のようになります。