液晶の弾性

弾性とは

液晶は弾性体として振る舞います。
こう聞いた時、液晶がどのように振る舞うのか理解できたでしょうか？
弾性体というと、いわゆるゴムのような伸びたり縮んだりする物質が思い浮かびます。
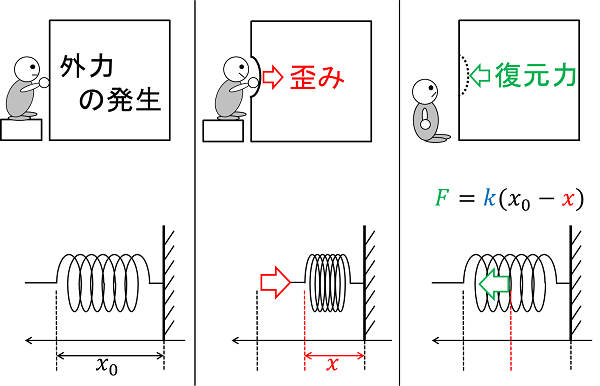
いわゆる弾性体は、外力によって変形しますが、外力が無くなった時には、
復元力によって元の形状に戻っていきます。
この時の復元力Fは、定数kと変位量の積で計算されますが、このｋを弾性定数と呼びます。



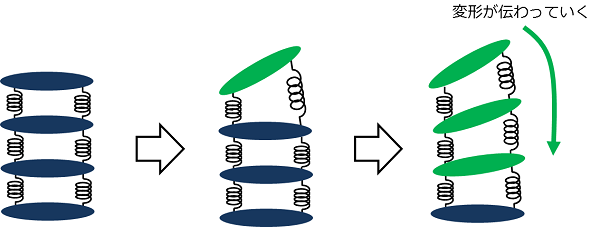
さて、液晶が弾性体というのはどういうことか、イメージを絵にするとこんな感じでしょうか？


どうでしょうか、液晶分子同士がバネで繋がったようなイメージです。
もちろん、基板に対しても、強目のバネで繋がっています。
この状態で、ある一つの分子が動いた（変形した）としましょう。どうなるでしょうか？
動いた分子に引きずられて、周りの分子にもバネを通してその影響が伝わっていきます。
これが液晶が有する弾性体としての振る舞いです。


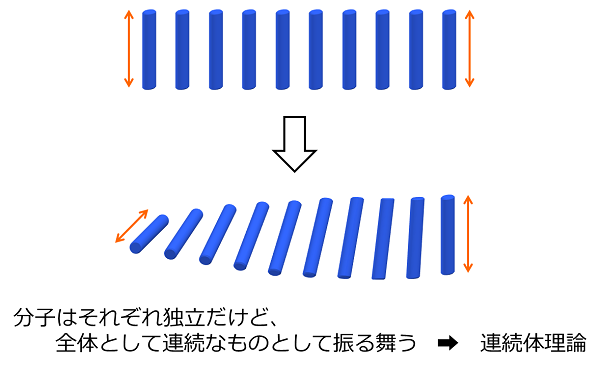
このように、ひとつひとつの分子は独立しているけれど、個々の分子が繋がりをもって振る舞う、
つまり、空間的に広がりを持ち、各分子が相互に影響を受けながら、
あたかもひとつに繋がっているかのように振る舞う事が、液晶が弾性体である所以です。
ちなみに、このように物質が存在する空間に対して連続的な振る舞いを見せる物質を、連続体と呼び、
その振る舞いを記述する理論を”連続体理論”といいます。

弾性定数

さて、弾性体として振る舞うことは分かりましたので、特性を示す値である弾性定数について考えましょう。
厳密に3次元の物質に対して弾性定数を定義すると、いろんな方向に対して弾性定数が出てきてしまって大変なので、
ここでは、1軸方向に配向したネマティック液晶での弾性定数を考えます。
ざっくり言うと、ネマティック液晶で出てくる弾性定数は3つです。
・広がり変形での弾性定数
・ねじれ変形での弾性定数
・曲がり変形での弾性定数
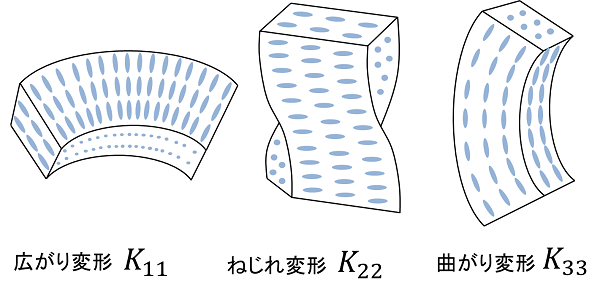
それぞれを絵で示すと次のようになります。

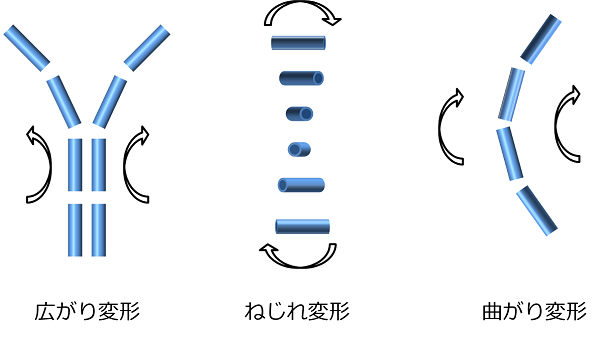
もう少し分子の集合体としての形のほうがわかりやすいかもしれません。
ちなみに、それぞれの弾性定数は、番号が振られています。
Ｋ1：広がり変形　（K11とも言います。）
Ｋ2：ねじれ変形　（K22とも言います。）
Ｋ3：曲がり変形　（K33とも言います。）




個人的な話ですが、
私が学生の頃、広がり変形は、分子の形状が広がっているから、広がり変形で、
曲がり変形は、分子形状が曲がるから、曲がり変形じゃないのかと思っていました。

正しくはダイレクタがどのように変形するかという定義ですから、
ダイレクタが広がるから、広がり変形。
ダイレクタがねじれるから、ねじれ変形。
ダイレクタが曲がるから、曲がり変形。
ということになります。

ダイレクタの変形と聞いてパッと分からなかったら、こう考えても同じことになります。
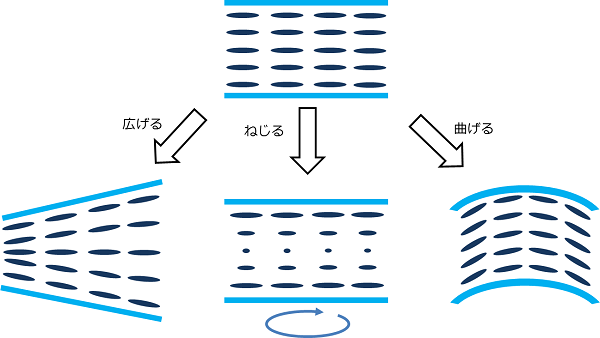
水平配向の液晶セルを用意したとき・・・、
液晶セルの基板を、広げた時に生じるのが広がり変形。
液晶セルの基板を、ねじった時に生じるのがねじれ変形。
液晶セルの基板を、曲げた時に生じるのが曲がり変形。



さて、ここまで弾性定数について説明してきました。
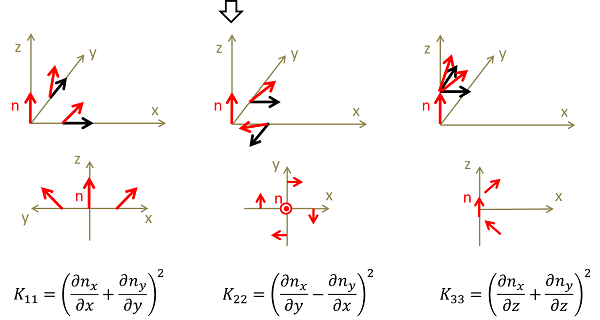
最後に、これら3つの弾性定数を数式にした時の、図と数式だけ示します。
ダイレクタｎが、z方向に配向しているとした時、各変形がどのように表されるかを示しています。