誘電率・屈折率の異方性
液晶は「異方性と流動性を兼ね備えた状態」と定義されました。
その異方性のために誘電率・屈折率にも異方性が存在する事になります。
まず、誘電率の異方性について話していきましょう。
そのためにまず誘電率とは何か？をお話しないといけませんね。 誘電率とは電場を加えた時に、「どれくらい電荷が偏りやすいか」を表した係数です。
液晶状態を有する物質は誘電体です。誘電体とは言い換えると電気を通さない絶縁体です。
電場を加えても電気は通さない。しかし物質内部では電場の大きさと誘電率の大きさに従った電荷の偏りが起こるのです。
つまり電荷の偏りやすさをあらわすのが誘電率εです。
液晶分子１個が全く動かない状態では３次元的に異方的なので、直交座標系においてX軸、Y軸、Z軸と分けて考えたとき、ε X ε Y ε Zという ３方向に異方的な誘電率を考える事ができる。(二軸性の誘電率楕円体)
しかしネマチック相などの状態では液晶分子の短軸方向の回転運動が加わるため、短軸方向の誘電率は一様であると考える事ができます。(一軸性の誘電率楕円体)
さらに等方相のように液晶分子の回転運動に対する束縛が無くなった時には、長軸方向の回転運動も起こるため結果的にはどの方向の誘電率も一様と考える事ができます。(球状の誘電率楕円体)
このようにミクロな分子１個に対して誘電率を考える事もできますし、またマクロに(液晶分子の集合体)考えた場合でも、結晶相、液晶相、等方相の３つにおいて同様の考察を行うことが可能です。
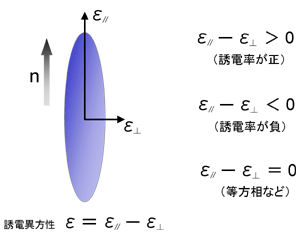図にあるように一軸性の誘電率楕円体(液晶分子の誘電率の偏りを楕円体として表したもの(正しくはありませんが模式的に液晶分子を表したものと考えてもらうと分かりやすいかと思います。)を長軸方向(ダイレクタ方向)と短軸方向に分けて考えた時、長軸方向の誘電率ε〃
と短軸方向の誘電率ε⊥と各方向への誘電率を定義できます。このように誘電率を定義した時、長軸方向の誘電率と短軸方向の誘電率が同じ場合を誘電異方性が無い、いわゆる誘電的に等方性の物質といえます。
また、長軸方向の誘電率と短軸方向の誘電率が違う場合を誘電異方性があるといい、長軸方向の誘電率が大きい場合を「誘電異方性が正」といい、短軸方向の誘電率が大きい場合を「誘電異方性が負」といいます。
電荷の偏りは分子構造内の電子の偏りであるため、この誘電異方性の符号の違いは液晶分子の構造に依存しています。(分子構造内の電気陰性度の違いによる電子の偏りなど)
さあ、誘電率の異方性について分かってきたところで、誘電率の異方性と屈折率の異方性を結びつける非常に重要な式を示します。ε ∞＝ｎ2
εはさきほど説明した誘電率です。εに∞がくっついていますね。この∞が表す意味は、周波数が無限大である事を示しています。
周波数が無限大、つまり高周波であると言う事です。
高周波での誘電率とはどういうことか、それは電子分極に起因した誘電率であると言う事です。
そしてｎは屈折率です。
つまり電子分極に起因する誘電率は屈折率の２乗と等しいのです。
電子分極とは「分極とは」で説明したように、最も高周波において現れる分子内の分極です。
分子内、つまり分子一つ一つの中で分極が起きるということです。
（それに対して、分子の集合体が引き起こすマクロな分極が配向分極といえます）
したがって電子分極が起こる高周波での誘電率とは、分子一つ一つの誘電率ということです。
つまり、この式では、分子一つの誘電率は、分子一つの屈折率の２乗に等しいという事です。
したがって誘電率が異方的であるということは屈折率も異方的であるということを示している。
（もちろん分子それぞれが異方性を持っていても、それらがバラバラな方向を向いていれば全体として見た場合は異方性が無い状態です）
この屈折率の異方性が複屈折という現象を引き起こしているのです。
さて、屈折率にも異方性が存在するという事は、屈折率においても誘電率と同じく「屈折率楕円体」を考える事ができます。
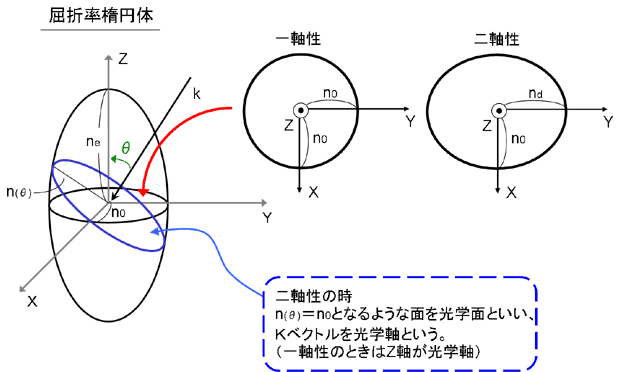
誘電率楕円体と同様に屈折率の異方性を屈折率楕円体によって表すと理解しやすい。
長軸方向をZ方向とした場合、短軸を含むXY平面で切った断面が円（ε X＝ε Y）であれば、一軸性の屈折率楕円体である。
また断面が楕円（ε X≠ε Y）であれば、二軸性の屈折率楕円体である。
また誘電率楕円体の場合と同じく、3方向の屈折率が全て等しい場合が屈折率楕円体が球状になる、つまり等方相という事です。
そして二軸性の場合、一軸性とは異なり図に示したようにZ軸方向から切っても円の断面になりません。
そこでｋ方向から断面を切り出したとき円の断面、つまり断面での屈折率が一様となる場合、そのｋ方向を光軸方向と言います。
つまり一軸性の屈折率楕円体においてはZ軸方向が光軸方向となります。
最後に液晶の誘電率・屈折率の測定法について少し述べておこうと思います。
誘電率の測定には、インピーダンスアナライザーという装置を用いて行います。
また屈折率の測定には、アッベの屈折計のような装置を用いて測定を行います。
どちらの装置においても、液晶が均一に配向、つまり液晶分子が全て同じ方向に向いていないと正確な値を測定する事ができません。
そのため、均一な配向が難しく、螺旋構造を取り、欠陥が発生する事で配向が乱れる強誘電性液晶のような液晶材料においては正確な誘電率・屈折率を測定する事が非常に困難を極めています。
したがって、強誘電液晶のような配向の難しい試料の屈折率や誘電率を定量的に測定を行なうためにコンピューターを用いた分子運動シュミレーションを行い屈折率や誘電率の測定を行なっています。
ここまで誘電率と屈折率の異方性について話してきました。
この異方性が液晶の物性を考える上で非常に重要になります。
特にディスプレイ応用、光を用いた応用においてこの２つの要素は非常に重要なのです。
また、液晶には誘電率・屈折率の異方性以外にも光学的・機械的・電気磁気的･･･etcなどの異方性が存在します。
これらの異方性を利用する事で、様々な応用が考えられており、液晶を用いた新たな技術が期待されています。